STL 常用容器 priority queue 详解
priority queue 概述
priority queue : 一种优先级队列,其允许用户以任何次序将元素压入容器内,与 queue 不同的是,从其中取出元素时是根据优先级顺序的。
priority queue 和 stack , queue 一样,只能算是适配器,并不能算是容器类。在介绍 priority queue 的底层容器之前,需要先了解 heap 这个数据结构。
heap : 堆,本质为完全二叉树(complete binary tree)。由完全二叉树的性质可得: 当用一个数组来从左到右,从上到下的顺序存放完全二叉树的元素时,一个元素位于 i 处时,其左子节点必位于 2i 处,其右子节点必位于 2i+1 处,其父节点必位于 i/2(取整) 处。 由此特性,我们可以使用数组来隐式地表示 heap 。
由于 heap 插入删除元素都有对数级的表现,并且由于其的隐式表示的便捷性,用其作为 priority queue 底层容器性价比最高。为了可扩展的方便, heap 一般用 vector 实现。注意:STL中的 heap 全部是 max_heap , 所以下文也全是 max-heap (父节点键值比子节点键值大)。
heap 算法
用 vector 来表示 heap 时,需要有两个迭代器 first 和 last 来表示可操作范围,即在 first 和 last 之间为 heap 的元素。
要弄清楚 priority queue 各个方法的底层实现时,必须先弄清楚 heap 的四个算法。
push_heap 算法
目的:将一个新元素插入已构建好的 heap 中。
步骤:
-
将新加入的元素放在最下层,从左至右的第一个空缺叶节点处,使加入新元素后的树仍为完全二叉树。
-
将新元素与其父节点比较键值大小,如果新元素大,则交换其与父节点的位置。
-
重复第二步,直至新元素小于父节点或新元素已位于根节点处。(上溯)
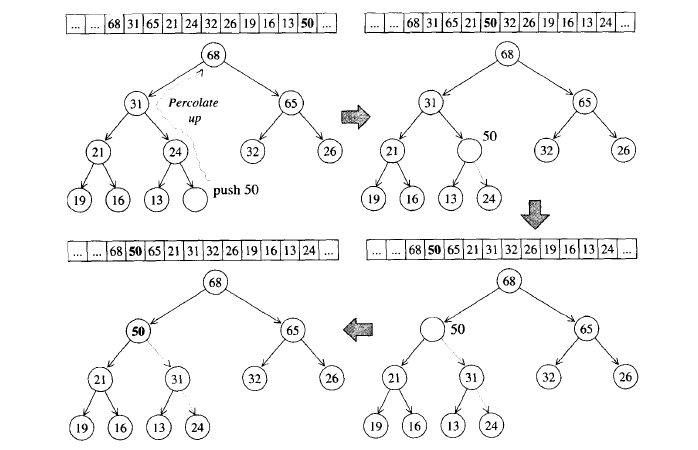
时间复杂度: 由于最坏情况是上溯到根节点,所以上溯次数最多是完全二叉树的深度。由完全二叉树的性质可得:其深度为 [log2n] + 1(向下取整)。所以 push_heap 算法的时间复杂度为 O(log2n) 。
pop_heap 算法
目的:将根节点取出树,并放置到 vector 可操作范围的最末端。
步骤:
-
将根节点取出,并将最后一个子节点放置到根节点位置, 称其为替补元素。 last 迭代器减一 ,然后将原来根节点的元素放置到 last 所指处。(本质是根节点与最后的子节点调换在 vector 中的位置)
-
将替补元素与其左右子节点中键值较大的一个做比较,如果替补元素键值小,则调换它们的位置。
-
重复第二步,直至替补元素无子节点或键值大于其所有子节点。(下溯)
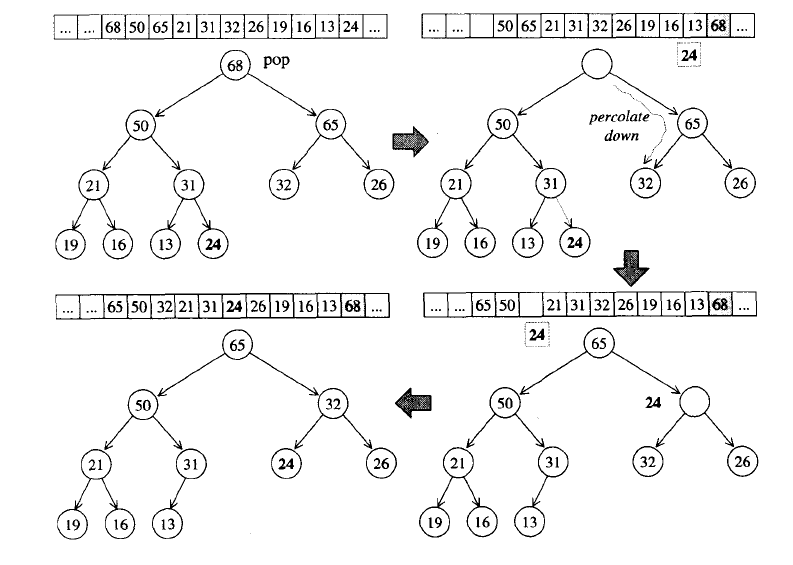
时间复杂度:同 push_heap ,其最坏情况是下溯到最底层。所以其时间复杂度为 O(log2n) 。
sort_heap 算法
目的:利用 pop_heap 每次都将键值最大的元素放置到可操作范围最末端,得到从小到大的排序序列。
步骤:
-
执行 pop_heap 算法。
-
重复第一步,直至可操作范围为0,即所有元素均被取出。
时间复杂度:因为执行了 n 步 pop_head 算法,所以时间复杂度为 O(nlog2n)
make_heap 算法
目的:将一段现有的数据转化为 heap。
步骤:
构建堆实质是一个不断调整子树,使得树满足堆的特性。
调整以非叶结点为单位,顺序是从后往前。调整的步骤为:如果调整节点比其最大的子节点小,则调换它们的顺序,并对下一个非叶节点进行调整。
时间复杂度:最坏的情况下需要遍历所有非叶节点才可以完成调整,非叶节点的个数为 n 数量级,所以时间复杂度为O(n)。
priority queue 方法
讲完 heap 的算法,再来看 priority queue 的实现已经非常简单了。
bool empty(); //判断是否非空
size_type size(); //返回容器大小
const_reference top(); //得到顶部元素的引用
void push(); //插入末端,按优先级重排 heap,底层使用 push_heap 算法
void pop(); //弹出优先级最高的元素,底层使用 pop_heap 算法
注意: 无论是 heap 还是 priority queue 都没有迭代器,因为它们都是按一定顺序来访问元素,不提供随机访问的方法。
后记
详细介绍了 priority queue 的实现方法,并分析了各种 heap 算法的时间复杂度。